在标准大气中当某点的电场达到大约3×105 V/m时,该点就会出现电子雪崩。理论上讲,这应该是放电的最初始发过程,但有关闪电始发条件的理论模式研究只把它当作前提而不把它作为研究对象。闪电始发条件的理论模式主要是研究放电始发后其持续发展条件和各种特性。闪电有正极性的,也有负极性的。各种实验研究表明:正极性放电比较单纯,但负极性放电非常复杂(见5.2节)。由于这个原因,有关正极性放电起始条件的模式研究较多,而有关负极性放电始发条件的模式几乎没有,在这一节里我们只介绍有关正极性放电始发条件的理论模式。在这些模式中,虽然有的模式是为了模拟长间隙放电而建立起来的(Gallimberti,1972;1979;Bondiou和Gallimberti,1994),但它们涉及到很多与闪电共通的基本物理过程,而且它们已被逐渐用到研究闪电的始发过程中,所以我们也把这些模式包括进去。
正流光持续传输的几个简化模式
正流光向前传输借助的是集中于它头部的正电荷团。正电荷团在它的前面产生强电场,从而在此发生强电离。电离后的电子与正离子受电场作用分离,电子与正电荷团发生中和而剩下的正离子汇集到一起就会形成新的正电荷团,这样正流光就向前传输相当于电荷团直径的一个距离。Dawson和Wimm(1965)将正流光头部的正电荷团假设成一个孤立的球。若新产生的正电荷团的半径与离子数能与老电荷团的半径及离子数等同,他们认为正流光就能持续传输。
新电荷团的半径
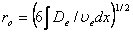 | (5-2) |
这里De是电子扩散系数, 是电子的迁移速度。
新电荷团的离子数
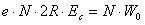
这里a是电离系数。
他们的计算结果表明:如果正流光头部的正电荷团的半径为30 μm,离子数为108,即使环境由场为0,该流光也能向前传输。后来Phelps(1971)根据他的实验结果对Dawson等人的模式进行了发展。Phelps认为当正流光在某一环境电场中传输时,若正流光从环境电场中获得的能量能补偿它传输时所损失的能量,那么该流光就可持续平衡地向前传输。若外部电场是0,正流光即使能传输一定的距离,由于损失的能量得不到补偿,正流光会很快终止。假定正电荷团的半径为R,离子数为N,流光每向前传输2R的距离,正流光从环境电场Ec中得到的能量e?N?2R?Ec。另一方面,流光每前进2R的距离,为使其平衡地向前传输,必须新电离出N个正离子。若每电离出一个正离子所需要的能量为W0(据实测,W0=30 eV),那么正流光每向前传输2R的距离所消耗掉的能量为NW。根据Phelps的理论可以得到以下正流光持续传输模式:
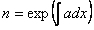 | (5-3) |
这个模式与他的实验结果非常吻合。
后来Wang和Guo(1989)通过分析上行雷产生时的电场环境,将Phelps的理论模式推广到可以解释正流光能在更低电场环境中持续传输的现象。他们认为正流光之所以转变成能在低电场环境中持续传输,靠的是一局部强环境的电场区域。当正流光通过该局部强电场区域时,流光从环境电场中得到的能量大于用来产生与老电荷团相同数目离子数所需要的能量,多出的能量将会产生出更多的离子,结果正流光头部的电荷团将变大。
根据式(5-3),若R变大,Ec就会变小。
基于上述分析,Wang和Guo(1989)得到一个关于R的方程式:
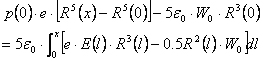 | (5-4) |
这里p(0)是初始流光头部的电荷密度, ,N(0)和R(0)分别是初始流光头部电荷团的离子数与半径。根据Dawson等人(1965)的研究,取N(0)=108,R(0)=30 μm。
结合式(5-3)和(5-4),Wang和Guo(1989)可以判断正流光能否在一环境电场中持续传输。他们的模式不仅能很好地说明上行雷,而且计算出的雷击距离与实测值也基本相符。
考虑到详细物理过程的正流光持续传输模式
在5.8.1中介绍到的几个模式仅从能量平衡的角度探讨了正流光持续传输的条件,而实际放电牵涉到很多物理过程,为了能够更好地模拟正流光持续传输现象,模式中必须考虑这些物理过程。Gallimberti(1972)提出的模式就考虑到了放电的一些基本物理过程。基于很多室内长间隙放电观测结果(Les Renardieres Group,1972),他把正流光头部的区域看成活性区,而把其后部的通道看成弱性区。只有在活性区才发生电离,也只有活性区直接关系到流光能否持续传输(见图5-24)。
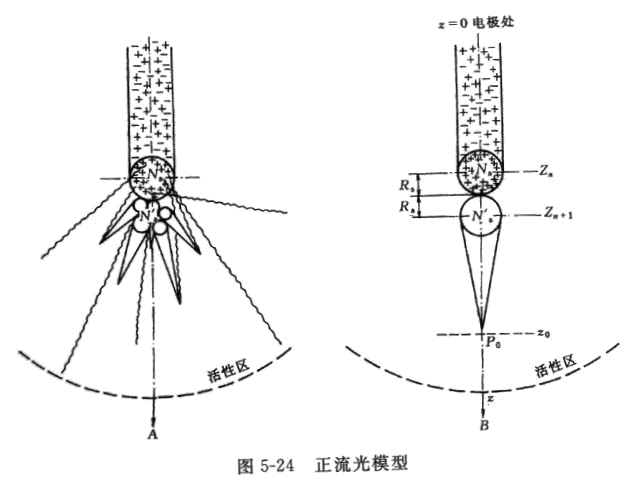
假定在某一时刻tn,流光头部半径为Rs,含有Ns个正离子和Ne个处于激发状态的分子。同时假定在活性区某点P0处由光电离引起的二次电子密度为nes(p)
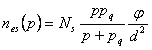 | (5-5) |
这里p和pq分别是气体的压强及淬灭压强,φ是光电子数与由电子雪崩产生的离子数的比率,d是点p0离开流光头部中心的距离。
活性区中的二次电子受强电场作用将产生一系列新的电子雪崩,如果tn时刻的二次电子密度,通过连续方程和泊松方程就可追踪一系列电子雪崩的发展状况直到tn+1时刻它们到达流光头部。这些方程可以归纳如下:
 | (5-6) |
这里ε是气体的介电常数,ne,nn和np分别是电子、负离子及正离子的密度;a和η分别是电离系数及分离系数;D和ve分别是电子的扩散系数及迁移速度。这些参数是环境电场的非线性函数。这些参数的大小可通过有关书籍查到。
这些方程的边界条件为
 | (5-7) |
以上这些方程就是Gallimberti推导出的描述流光传输的基本方程式。很遗憾的是这些方程式太复杂,现实中很难求解。因而Galimberti在他的模式中作了以下几点简化:
(1)把实际发生在流光头部处的众多电子雪崩简化成一个等价的电子雪崩,通过调节该电子雪崩的起始位置使它产生的空间电荷与众多电子雷崩产生的空间电荷相同。
(2)由于空间电荷的计算非常复杂,为了避免反复求解空间电荷,通过能量守恒原理来计算等价电子雪崩的起始点位置。
(3)把所有方程简化到一维空间。这样(4)式的连续方程简化到z轴方向就变成:
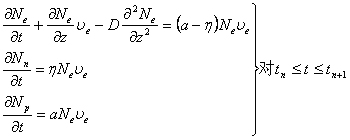 | (5-8) |
这里N(z,t)是沿z轴方向的线密度。
(4)空间电场E(z)由外部环境电场和流光头部电荷团产生的电场组成:
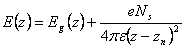 | (5-9) |
(5)流光头部的半径R等于电子径向位移的平方根
 | (5-10) |
(6)流光新头部的离子数
 | (5-11) |
这里z0是电子雪崩的起始点。
(7)等价流光的形成时间ta
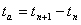 | (5-12) |
(8)在一系列电子雪崩形成过程中,若从环境电场中得到的能量为Wg,损耗的能量为W1,流光老头部与新头部的势能差为ΔWpot,根据能量平衡原理:
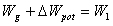 | (5-13) |
并且Wg,W1及ΔWpot可以分别用下列公式求出:
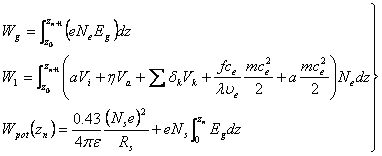 | (5-14) |
这里Vi及Va分别是电离能和共振附着能,δk是能级Vk的激发系数,ce是电子均方速度的平方根,λ是电子的自由程,f是电子和气体分子弹性碰撞时损失掉的能量的百分比。
在式(5-13)中,W1须考虑到电离、附着、振动、电子激发、散乱等造成的损失,Wpot须考虑到电荷聚集及外场的势能。
在Gatlimberti的模式中,等价电子雪崩的起始点位置需要同时满足连续方程式(5-8)及能量平衡方程(5-13)。通过反复数值试验可以求出这个等价电子雪崩的起始点位置。判断流光是否能持续传输的条件是:若等价电子雪崩起始点处的电场大于2.6×106 V/m,那么流光就可持续传输;反之,流光则中止。
Gallimberti用他的模式对实际长间隙放电进行了模拟,并与实测结果进行了比较,图5-25是一例有关流光长度与时间关系的结果。图中实线代表理论计算值,空心点是实测数据。可以看到模式结果与实测结果非常吻合。图5-26是一例有关间隙起始电压与流光长度关系的结果。实线代表理论计算值,空心点是实测数据,同样可以看到模式结果与实测结果非常一致。
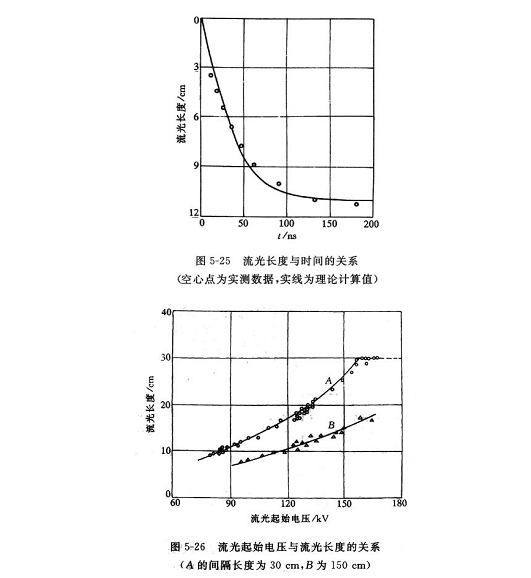
用Gallimberti的流光模式还可以计算流光电流、流光头部离子数等。现在他的模式在欧洲已被广泛地利用。
考虑到详细物理过程的正先导模式
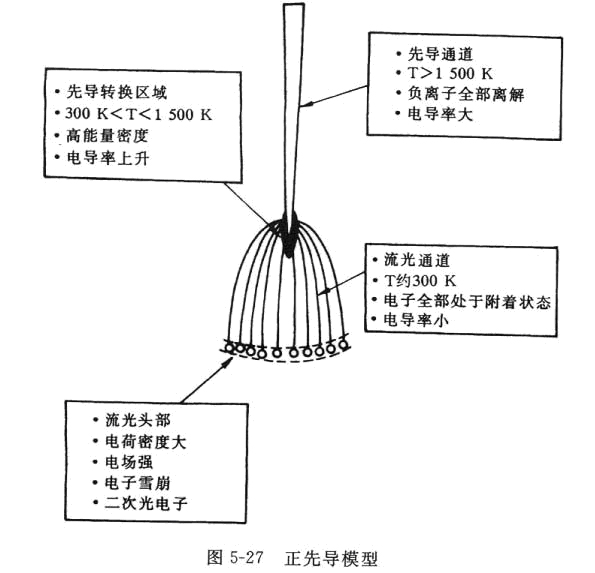
当流光发展到一定程度,受众多丝状流光通道中电流的加热作用,流光根部温度将达到1500至2000K。此时根部处的负离子将被解离,因而导电度也将大增,最终流光转变成先导。在这一过程中焦耳热量将转变成分子的振动、转动及激发能等。
流光??先导系统向前传输的过程可以用图5-27的模型来说明。由于发生于流光顶部处的电子雪崩,在流光顶部形成空间电荷,这些空间电荷又为产生新的电子雪崩提供强电场;流光丝状通道电流洪到一起形成先导电流,而先导电流又为流光持续发展提供足够的环境电场;由此可以看到先导与流光形成一耦合系统,两者相辅相成。
Gallimberti(1979)分析了流光转变成先导及先导向前传输时各种形式能量之间的转换过程,并建立了一系列状态平衡方程、粒子连续方程及能量平衡方程等。由于这些方程非常复杂,这里我们不作引用,有兴趣的读者可参照原文。Gallimberti根据他所建立的方程再加上一些近似处理,可以计算诸如先导电流、先导电离度等。他的计算结果能很好地说明20世纪70年代欧洲不同国家众多研究机构联合起来观测到的室内长间隙放电实验结果(Les Renardieres Group,1972;1974;1977;1981)。
最近,Bondiou和Gallimberti(1994a)把以上所述Gallimberti的流光模式及先导模式全部组合到一起,并作进一步简化处理后建立了一个很系统的正先导模式。这个模式的特点是:只要给出长间隙的结构及所加高电压的波形,它就可以一步一步地计算出各种放电参量,直到最终击穿发生。在这个模式中,在某一步计算出的空间电荷、电场及温度分布等结果将是下一步计算时的输入数据。利用这个模式可以计算初始电晕放电及流光的起始时间、流光转变成先导的时间、先导电流、先导速度、先导中的电场分布、击穿发生时间、50%击穿电压等等。他们的计算结果与长间隙放电实测结果基本相符。
最近,Bondiou和Gallimberti的模式被进一步简化,并被用于模拟人工引雷的初始上行先导(Bondiou等,1994b,1999)。在模拟长间隙放电时,先导电流只有几安培,先导的温度较低,因而不需要考虑热电离。对于人工引雷的上行先导,其电流可大到几十安培甚至几百安培,这时先导的温度可达6000 K,因此需要考虑热电离。他们假定热电离满足局部热平衡条件,从而得出先导内的电场甚小,可以忽略不计。另外在模拟长间隙放电时,外部电场比较容易计算,而在模拟人工引雷时,受电场诱导作用,导线上的电荷分布较复杂。他们利用了一种电荷模拟法的子程序解决了这个问题。现在,他们的模式已经很好地模拟人工引雷初始过程中所观测到的脉冲电流。他们认为,对于人工引雷,外部环境电场较低,流光??先导系统不可能与外部环境电场达到平衡状态,因而人工引雷中的初始上行正先导是不连续的(即脉冲式)。在先导的顶端,由于那里的电场很强,流光将以很快的速度向前传输到低环境电场中,电离也就中止。
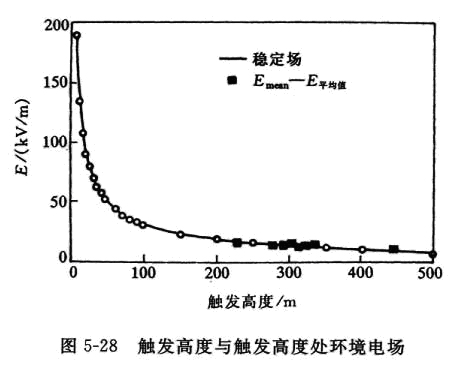
另外,他们通过模式计算得到了一个触发高度与环境电场之间的关系(见图5-28)。图5-28中的小黑方块对应的是实测数据。可以看到他们的模式基本上与实测结果一致。
考虑到云中特殊环境的理论模式
云中含有大量冰晶,也含有大量水滴等,它们不仅大小不一而且可以有各种各样的形状。它们在气流之中会发生各种运动及碰撞,且本身也带有电荷。这些因素都会影响到云中闪电的起始过程,因而有关理论模式也应考虑这方面的因素。
Nguyen和Michnowski(1996)最近提出的一种模式认为,与两个水滴之间受某一突发因素发生放电时,它们附件空间中的电场会瞬时地变强,从而导致附近水滴之间的放电,通过这样的连锁反应,放电就可在较低的环境电场中传输。这个理论模式对理解闪电通道在云中的最初形成过程可能会有一定的价值。

